
Review Differentiation Of Exponential Functions Ppt Download
It is unclear or not useful Bookmark this question Show activity on this post I am trying to see why E E X Y = E X for joint variables X and Y I understand the following E X = ∫ − ∞ ∞ x f X ( x) d xCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
Y=(e^x-e^-x)/(e^x+e^-x) derivative
Y=(e^x-e^-x)/(e^x+e^-x) derivative-This question shows research effort;\\frac{d}{dx} \frac{{e}^{x}{e}^{x}}{{e}^{x}{e}^{x}}\ > <
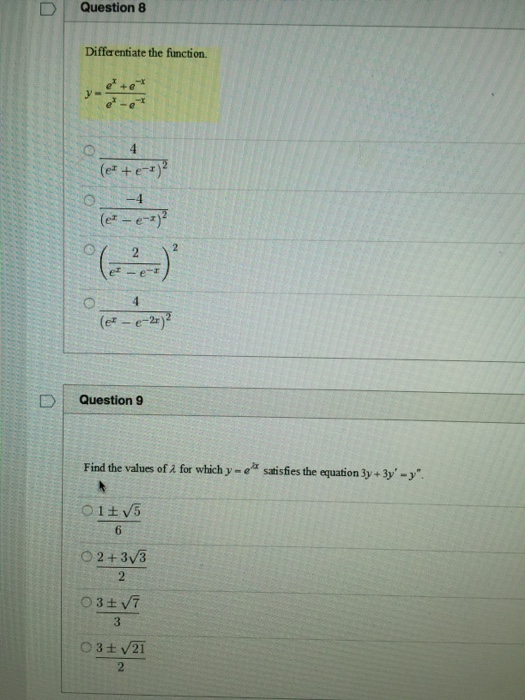
Solved Differentiate The Function Y E X E X E X E X Chegg Com
Here y CF = c 1 e x c 2 xe x Since the right hand member of the complete equation is X(x) = e x, therefore the first possible assumption for particular integral would be y PI = Ae x, but this solution has already occurred in y CFWe, therefore, y PI(x) = Axe xStill this solution also has appeared in y CFWe, therefore, again multiply by x and try y PI (x) = Ax 2 e xSolutionShow Solution y = e x x e x x Taking the logarithm of both sides, we get log y = log e x x x x e e x x = x x log e ∴ log y = x x x x Differentiating both sides wrtx, we get y dy dx d dx x x 1 y ⋅ dy dx = d dx ( x x) (i) Let u = x x x xIt can be solved by simple manipulation e^x e^ {x} = 3e^x 3e^ {x} 2e^x 4e^ {x} = 0 e^x 2e^ {x} = 0 e^ {2x} = 2 \ln {e^ {2x}} = \ln {2} 2x = \ln {2} x = \dfrac {\ln {2}} {2} It can be solved by simple manipulation ex e−x = 3ex −3e−x −2ex 4e−x =
The derivative of e to the x times we're multiplying both sides by e to the x, times e to the x over e to the x I just chose to put the e to the x on this term, is equal to e to the x This is 1 Scratch it out We're done That might not have been completely satisfying for you, but it works The derivative of e to the x is equal to e to the xThe Derivative of e x We consider the series expression for the exponential function We can calculate the derivative of the left side by applying the rule for the derivative of a sum That is, the derivative of a sum equals the sum of the derivatives of each term I added an extra term to make the pattern clearDy/dx = (dy/dm)*(dm/dx) = (e^m)ln(x)1(x^x) = yln(x)1(x^x) = (e^x^x)ln(x)1(x^x) So dy/dx (the derivative of e^x^x with respect to x) = ln(x)1(x^x)(e^x^x) 9 4
Y=(e^x-e^-x)/(e^x+e^-x) derivativeのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 | ||
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 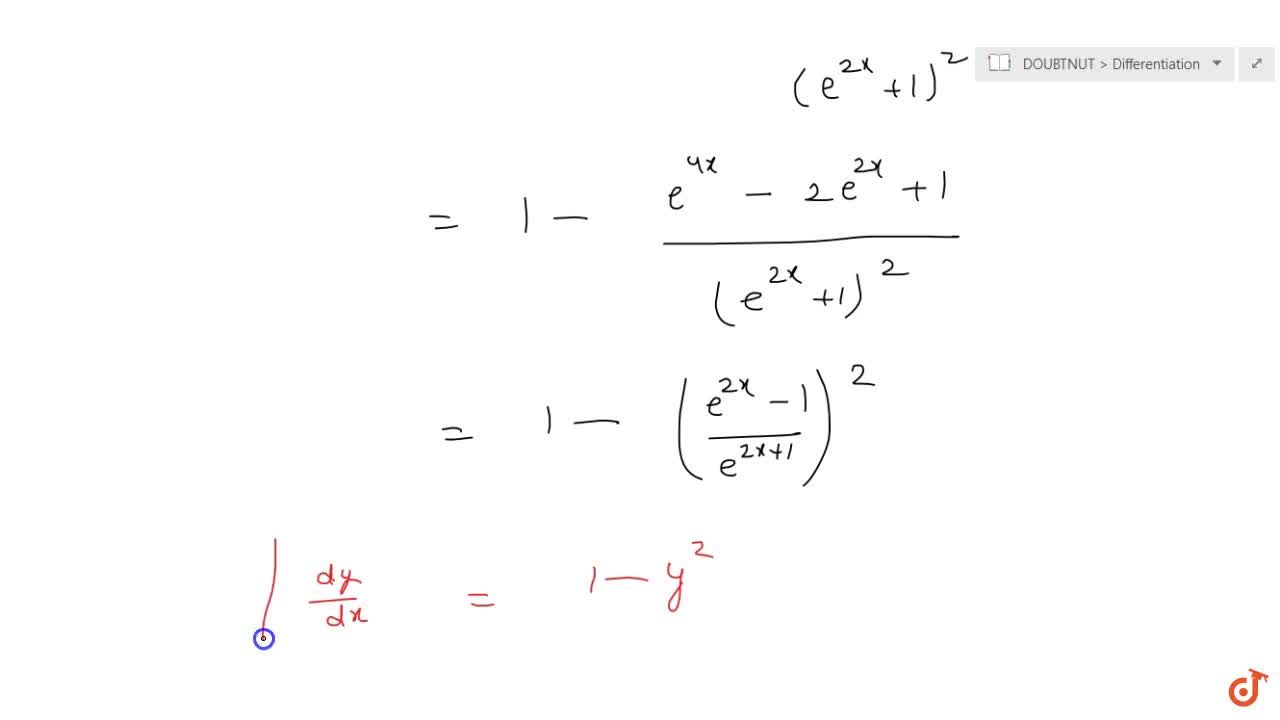 |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
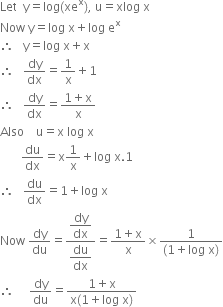 |  | |
 |  | |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
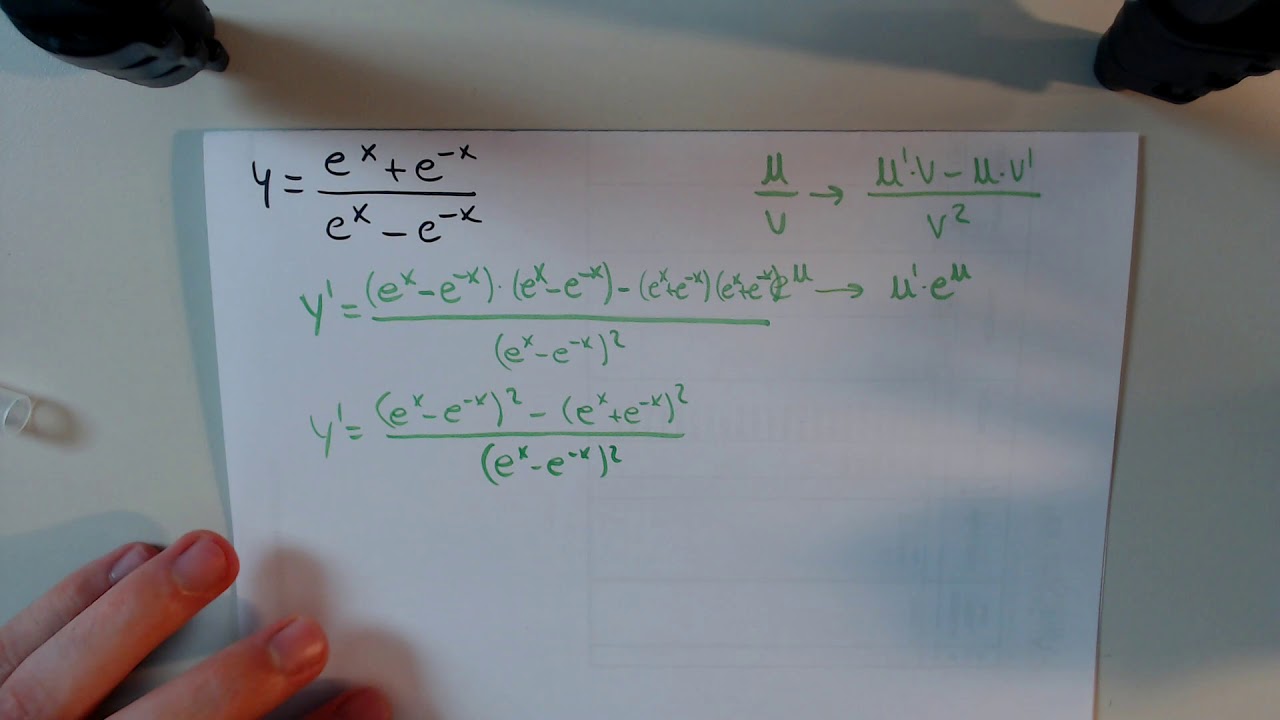 |  | |
 |  | |
 |  | |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | 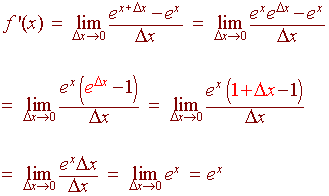 |  |
「Y=(e^x-e^-x)/(e^x+e^-x) derivative」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 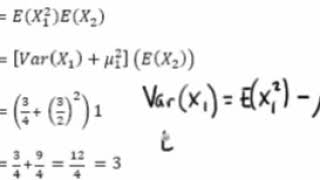 |
 |
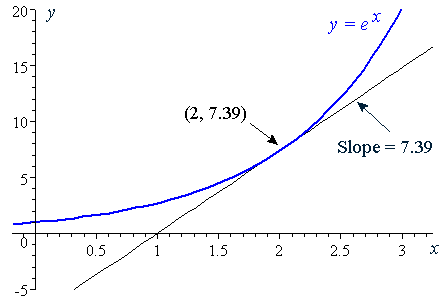
That is, e x!`(d(e^x))/(dx)=e^x` What does this mean?
Incoming Term: y=(e^x-e^-x)/(e^x+e^-x) derivative,




0 件のコメント:
コメントを投稿